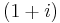Annuity (finance theory)
The term annuity is used in finance theory to refer to any terminating stream of fixed payments over a specified period of time. [1] This usage is most commonly seen in discussions of finance, usually in connection with the valuation of the stream of payments, taking into account time value of money concepts such as interest rate and future value.[2]
Examples of annuities are regular deposits to a savings account, monthly home mortgage payments and monthly insurance payments. [3]Annuities are classified by the frequency of payment dates. The payments (deposits) may be made weekly, monthly, quarterly, yearly, or at any other interval of time.
Contents |
Ordinary annuity
An ordinary annuity (also referred as annuity-immediate) is an annuity whose payments are made at the end of each period (e.g. a month, a year). The values of an ordinary annuity can be calculated through the following:[4]
Let:
 = the yearly nominal interest rate.
= the yearly nominal interest rate. = the number of years.
= the number of years. = the number of periods per year.
= the number of periods per year. = the interest rate per period.
= the interest rate per period. = the number of periods.
= the number of periods.
Note:
Also let:
 = the principal (or present value).
= the principal (or present value). = the future value of an annuity.
= the future value of an annuity. = the periodic payment in an annuity (the amortized payment).
= the periodic payment in an annuity (the amortized payment).
Also:
Clearly, in the limit as  increases,
increases,
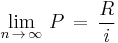
Thus, even an infinite series of finite payments (perpetuity) with a non-zero discount rate has a finite present value.
Proof
The next payment is to be paid in one period. Thus, the present value is computed to be:
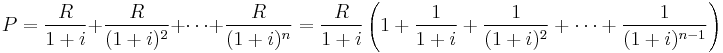 .
.
We notice that the second factor is a geometric progression of scale factor 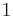 and of common ratio
and of common ratio 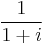 . We can write
. We can write
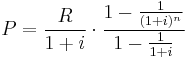 .
.
Finally, after simplifications, we obtain
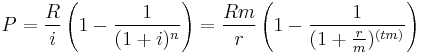 .
.
Similarly, we can prove the formula for the future value. The payment made at the end of the last year would accumulate no interest and the payment made at the end of the first year would accumulate interest for a total of (n−1) years. Therefore,
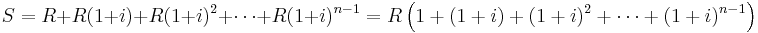 .
.
Hence:
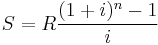 .
.
Additional formula
If an annuity is for repaying a debt P with interest, the amount owed after n payments is:
because the scheme is equivalent with lending an amount 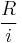 and putting part of that, an amount
and putting part of that, an amount 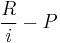 , in the bank to grow due to interest. See also fixed rate mortgage.
, in the bank to grow due to interest. See also fixed rate mortgage.
Also, this can be thought of as the present value of the remaining payments: ![R\left[ \frac{1}{i}-\frac{(i%2B1)^{n-N}}{i} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/f10e0226ef4bdf72c2a243292c27c0b9.png)
Annuity-due
An annuity-due is an annuity whose payments are made at the beginning of each period.[5] Deposits in savings, rent or lease payments, and insurance premiums are examples of annuities due.
Because each annuity payment is allowed to compound for one extra period, the value of an annuity-due is equal to the value of the corresponding ordinary annuity multiplied by (1+i). Thus, the future value of an annuity-due can be calculated through the formula (variables named as above):[4]
It can also be written as
An annuity-due with n payments is the sum of one annuity payment now and an ordinary annuity with one payment less, and also equal, with a time shift, to an ordinary annuity with one payment more, minus the last payment.
Thus we have:
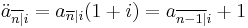 (value at the time of the first of n payments of 1)
(value at the time of the first of n payments of 1)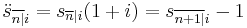 (value one period after the time of the last of n payments of 1)
(value one period after the time of the last of n payments of 1)
Formula for Finding the Periodic payment(R), Given A:
R = A/(1+〖(1-(1+(j/m) )〗^(-(n-1))/(j/m))
Examples: 1. Find the periodic payment of an annuity due of $70000, payable annually for 3 years at 15% compounded annually. R= 70000/(1+〖(1-(1+((.15)/1) )〗^(-(3-1))/((.15)/1)) R = 70000/2.625708885 R = $26659.46724
2. Find the periodic payment of an annuity due of $250700, payable quarterly for 8 years at 5% compounded quarterly. R= 250700/(1+〖(1-(1+((.05)/4) )〗^(-(32-1))/((.05)/4)) R = 250700/26.5692901 R = $9435.71
Finding the Periodic Payment(R), Given S:
R = S\,/((〖((1+(j/m) )〗^(n+1)-1)/(j/m)-1)
Examples: 1. Find the periodic payment of an accumulated value of $55000, payable monthly for 3 years at 15% compounded monthly. R=55000/((〖((1+((.15)/12) )〗^(36+1)-1)/((.15)/12)-1) R = 55000/45.67944932 R = $1204.04
2. Find the periodic payment of an accumulated value of $1600000, payable annually for 3 years at 9% compounded annually. R=1600000/((〖((1+((.09)/1) )〗^(3+1)-1)/((.09)/1)-1) R = 1600000/3.573129 R = $447786.80
Other types
- Fixed annuities – These are annuities with fixed payments. They are primarily used for low risk investments like government securities or corporate bonds. Fixed annuities offer a fixed rate but are not regulated by the Securities and Exchange Commission. This type can be adversely affected by high inflation.
- Variable annuities – Unlike fixed annuities, these are regulated by the SEC. They allow you to invest in portions of money markets.
- Equity-indexed annuities – Lump sum payments are made to an insurance company. Can be implemented with a Call option.
See also
References
- ^ Gibson, Eloise. "Explaining Annuities". Business Day. http://www.stuff.co.nz/business/money/5565136/Explaining-annuities. Retrieved 05/09/11.
- ^ Lasher, William (2008). Practical financial management. Mason, Ohio: Thomson South-Western. p. 230. ISBN 0-324-42262-8.
- ^ http://www.americanchronicle.com/articles/yb/157187005
- ^ a b Finite Mathematics, Eighth Edition, by Margaret L. Lial, Raymond N. Greenwell, and Nathan P. Ritchey. Published by Addison Wesley. ISBN 032122826X
- ^ Jordan, Bradford D.; Ross, Stephen David; Westerfield, Randolph (2000). Fundamentals of corporate finance. Boston: Irwin/McGraw-Hill. p. 175. ISBN 0-07-231289-0.
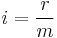
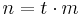
![S \,=\,R\left[\frac{\left(1%2Bi\right)^n-1}{i}\right] \,=\,R\cdot s_{\overline{n}|i}](/2012-wikipedia_en_all_nopic_01_2012/I/b379656fb39e787145ba8c59624c49a1.png) (
(![P \,=\,R\left[\frac{1-\left(1%2Bi\right)^{-n}}{i}\right] = R\cdot a_{\overline{n}|i}](/2012-wikipedia_en_all_nopic_01_2012/I/6e16914c864f8fa0f67242b3778152e0.png)
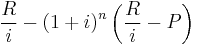
![S \, = \, R \left[ { (1%2Bi)^{n%2B1} - 1 \over i } \right] - R\,=\,R\cdot \ddot{s}_{\overline{n|}i}](/2012-wikipedia_en_all_nopic_01_2012/I/e009e72ece5798791d1ddd8eeb90d464.png) (
(
\,=\,R\cdot s_{\overline{n}|i}](/2012-wikipedia_en_all_nopic_01_2012/I/67ee872d0e165a7d9a33b45fe550aa2b.png)